ロマンティック数学ナイト

※本セミナーは終了しましたが、数学教室和(なごみ)での個別授業で受講可能です。以下のリンクからお問い合わせください。
⇒数学教室和(なごみ) お問い合わせフォーム

「ルベーグ積分を１から学んでみよう」というコンセプトのロマ数トレラン「ルベーグ積分入門セミナー」ですが、第１期が満員御礼、好評につき、第２期を開講します。

※無料ガイダンス回へのお申し込みはこちらから
ガイダンス回お申し込みフォーム

∞セミナーの概略∞

高校数学でも学ぶように，積分はグラフで囲まれた部分の面積を求める際に便利です．まずはリーマン積分とルベーグ積分について簡単に説明しましょう．

1) リーマン積分

大学初年時の微分積分学の授業で多くの人が学ぶ積分は，長方形で図形を近似して面積を求めるもので「リーマン(Riemann) 積分」と呼ばれています．

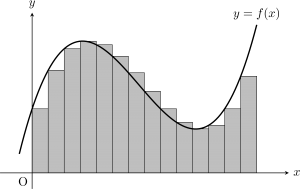
高校数学で学ぶ積分もリーマン積分の考え方をもとにしており，単純で分かりやすい積分です．しかし，リーマン積分は

・「完備性」をもたないこと
・「極限と積分の順序交換のための条件」が面倒(一様収束性が必要)

など数学的には少々扱いづらいという欠点があります．(もちろんこれらの内容についてもセミナーで説明します)．

2) ルベーグ積分

1902 年，フランスの博士課程の学生だったアンリ・ルベーグ(Henri Lebesgue) は博士論文を提出します．この博士論文では積分に関する新たな考え方がまとめられており， これが「ルベーグ(Lebesgue) 積分」の始まりとなります．このルベーグ積分はリーマン積分の欠点を大きく改善しており，数学的にも非常に扱いやすいものとなっています．このため，現代の数学の研究に現れる積分のほとんどで，積分はルベーグ積分で行います．

加えて，リーマン積分では計算できなかったものもルベーグ積分では計算できることもあります．たとえば
\[
f(x)=\begin{cases}1&(\text{$x$は有理数})\\0&(\text{$x$は無理数})\end{cases}
\]
という関数\(f\)を考えましょう．この関数\(f\)は「ディリクレ(Dirichlet) 関数」と呼ばれています．このディリクレ関数\(f\)は
\[
\begin{eqnarray*}
f\left(4\right)&=&f\left(\frac{1}{2}\right)=f\left(\frac{4}{3}\right)=1\\
f\left(-\sqrt{2}\right)&=&f\left(\pi\right)=f\left(\log_{2}{5}\right)=0
\end{eqnarray*}
\]
のように，有理数を代入すると\(1\)を返し，無理数を代入すると\(0\)を返すような関数です．

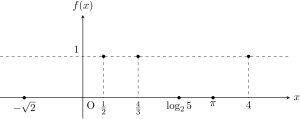
といっても，多くの方がピンとこないかも知れませんね．無理数と有理数は極めて細かく入り組んでいることが知られており，ディリクレ関数\(y=f(x)\)のグラフは\(0\)と\(1\)を非常に細かく「往復」するグラフになります．

実は，Dirichlet 関数の\(0\)と\(1\)の「往復」はあまりにも細かいため，リーマン積分することができません．しかし，ルベーグ積分をすることは可能で，なんと値が\(0\)と求まります! ルベーグ積分を考えると，こんなぐちゃぐちゃな関数でも「面積」に相当するものを考えることができるのです．このことは無料の第0 回(ガイダンス回) でも触れますので是非お越しください．

3) 本セミナーの目標

さて，先ほど説明したようにルベーグ積分では「極限と積分の順序交換のための条件」がリーマン積分よりも扱いやすくなっています．この条件を述べた定理をルベーグの優収束定理(dominated convergence theorem)といい，この定理はもはやルベーグ積分を扱う大きなメリットとなる定理です．本セミナーでは，このルベーグの優収束定理を理解し使えるようになることを目標とします．
たとえば

・関数解析
・測度論(確率論)
・偏微分方程式

など解析学の多くの分野では極限，微分，積分を主な道具として使います．そのため，極限と積分が同時に現れることもよくあり，これらの順序交換をしたい機会が多く現れます．ルベーグの優収束定理を使えるようになっていれば，これらの分野にも恐れることなく学んでいくことができます．

※セミナー内容について山本先生の書下ろし記事があります。こちらも是非お読みください！
https://wakara.co.jp/mathlog/20200904_2

∞セミナーの形式∞

テキスト「ルベグ積分入門」(吉田洋一著，ちくま学芸文庫) をもとにセミナーを進めます．本セミナーは

・授業パート
・演習パート

の２パートに分けて進めます．

授業の最後にその回の内容についての宿題を出しますので，次回のセミナーまでにこなしてきてください．もちろん受講生LINE グループでわいわい相談しながら解いてくださって構いません．というより，むしろその方が力は付くと思います．

宿題を授業の最初に各自の解答を持ち寄り，考え方を共有していきます．その際，解けたにしても解けなかったにしても，「考えたこと」や「試してみたこと」などまで共有できるのが好ましいです．

数学は数式が先にあるのではありません．「やりたいこと」が先にあり，数式はそれを表現するためにあるのです．ですから，「どう考えたか」「何をしたかったか」を受講生同士で共有できるセミナーを目指します．

∞受講対象∞

・ルベーグ積分に興味のある方
・高校数学をある程度知っている(勉強した) ことがある方
・集合の書き方に慣れている方(が好ましい)
・テキスト「ルベグ積分入門(https://amzn.to/2E0TTtx)」を入手できる方

∞セミナー内容∞

・リーマン積分はどのような積分か
・ルベーグ積分はなぜ必要か
・セミナーで用いる基礎事項(集合・写像・極限)
・線分の「長さ」はどう測る? (完全加法族，測度)
・ルベーグ積分の「長さ」(外測度，ルベーグ可測な集合，ルベーグ測度)
・ルベーグ積分ができる関数(ルベーグ可測な関数)
・ルベーグ積分の定義と性質
・Lebesgue の優収束定理
・リーマン積分とルベーグ積分の関係

∞セミナー講師∞

山本拓人(やまもとたくと)

・塾、予備校業界で約10 年の指導歴を持つ．受験指導に関しては，塾講師1 年目で府内トップ校への合格者を輩出させたり，個別指導2 年目で国公立大学医学部への合格者を輩出したり，家庭教師で偏差値を15上げて有名私立中学に合格させるなど，講師を始めた頃から早くも指導力を発揮し始める．その後も指導力に磨きをかけ，予備校1年目の生徒アンケートでベテランを凌ぐトップクラスの高評価を得て通常の8倍の報酬アップを提示される．

・「大人のための数学教室和」の大阪校で講師を務め，体験授業を受講した方の90% 以上が入会しており，お客様のレベルに合わせた痒いところに手が届く説明には定評がある．個別授業では主に大学数学・統計学・統計検定対策を指導し，大阪校での「統計超入門セミナー」の講師も務める．

・解説記事を執筆する数学ブロガーでもあり，大学受験ブログ・大学数学ブログの月刊閲覧数は7 万を超える．最近はYouTube に力を入れ始めている．

・大学院修士課程に飛び級で首席合格するなど，数学に対する知識・理解も深い．専門は非線形偏微分方程式で，現在は京都大学内にある数理解析研究所(RIMS) にて博士後期課程として数学の研究を行っている．

・趣味はピアノ，スポーツ，甘いもの食べ歩き．犬猫派．

∞開催場所∞

オンライン(zoom)

※好きな場所でご受講できます。「zoom」を用いてオンラインでセミナーを行います。
※ブラウザが利用できるPCやタブレットなどの環境をご用意ください。
※iPad等タブレットの使用は一部機能が制限される場合がございます。パソコン端末でのご参加を推奨いたします。

∞開催日時∞

第0回2021年3月20日(土) 14時30分～16時00分（ガイダンス回・無料）
第1回 4月10日(土) 14時30分～17時00分
第2回 4月24日(土) 14時30分～17時00分
第3回 5月8日(土) 14時30分～17時00分
第4回 5月22日(土) 14時30分～17時00分
第5回 6月5日(土) 14時30分～17時00分
第6回 6月26日(土) 14時30分～17時00分 ※例外的に3週間後
第7回 7月10日(土) 14時30分～17時00分
第8回 7月24日(土) 14時30分～17時00分
第9回 8月7日(土) 14時30分～17時00分
第10回 8月21日(土) 14時30分～17時00分

※3月20日の第0回は4月10日開講の本セミナーのガイダンス回となります。
※第0回に参加しなくても第1回目以降は申し込むことは可能です。
※セミナー時間150分の内、30分は受講生からの質問、議論に充てられるように設計しています。
※各セミナーの録画をゼミ最終回の1か月後まで視聴できるようにしますので、欠席の回があっても問題ありません。

∞お持ち物∞

筆記用具（ペン、ノートなど）

∞料金とお申し込みに関して∞

・ガイダンス回(3月20日)  無料
⇒お申込み(googleフォーム)
・本セミナー(全10回) 65,500円(早期割引:62,500円)
⇒お申込み(googleフォーム)

※セミナーの性格上本セミナーの定員は8名とさせていただきます(先着順)。
※本セミナーお申し込みの方に振込先の口座をご連絡いたします。
※最小履行人数は4名となります。最小履行人数に満たない場合、非開催となり、料金は返金させていただきます。開催有無は第一回ゼミの7日前である4月3日に確定となります。
※早期割引はガイダンス回翌日までに全回お申し込みの方に適用いたします。
※日程、時間の都合でガイダンス回に参加できない方は、担当の松中(メール：class@wakara.co.jp)までご連絡ください。ガイダンス回当日中に録画した動画を視聴できるように手配いたします。ただし、早期割引が適用されるのはガイダンス回の翌日までとなりますので、予めご了承ください。

∞本セミナー受講希望者の方向けの注意事項∞

・通信トラブル等が発生した時に、講師、受講生で円滑に連絡を取り合えるようLINEグループを作成します。LINEグループへの参加は必須とさせていただきますので、予めご了承ください。
・オンラインセミナー受講の際に必要となるパソコン、タブレットまたはスマホ等の通信機器、およびWiFi等のインターネット接続サービスは受講生ご自身でご準備いただきます。
・各セミナーの録画動画を最終回の1か月後まで視聴できるようにしますので、出席できない回は動画での受講が可能です。
・欠席者には録画動画だけでなく、セミナーで使用する配布資料(pdfファイルやurl等)も出席者同様配布いたします。

∞ロマ数トレランとは∞

「時間はかかってもいいから数学の美しさを中身からしっかり理解したい！」
聞いているだけでわくわくする華やかなテーマが満載のロマンティック数学ゼミ。
その根底となる理論からしっかり学びたい。ロマ数トレランはそんな声から生まれました。

ロマ数トレランは、ロマン溢れる数学を語ることができる講師による、講義形式ではなく、双方向の対話に重きをおいた受講者参加型の少人数制ゼミです。
実際に手を動かしたり、しっかりと質問、議論をする時間を設けることで
内容を確実に理解することを目標とします。同じ気持ちをもった仲間と一緒に学んだ先には新しい数学の世界が待っています。

～トレランとは～
山を縦走する山岳レースを意味するトレイルランニングの略です。
急坂は大変な時はありますが、いったん頂上に上がれば壮大な風景を楽しむことができます。
数学も同じです！平坦な道も、下り坂も、そして時にはハードな時もありますが、頑張って登りきれば素晴らしい風景が広がっているのです！

※ロマ数トレランでは受講生の理解に合わせて講師が適切な速度になるよう誘導しますが、受講者の理解を優先するため、カリキュラムの進度は確約いたしかねますので、予めご了承ください。
※質問の内容がセミナーの趣旨とそれる場合や、セミナーの適切な進行の妨げになると講師が判断した場合には、解説はセミナー内ではなく別途個別指導をご受講いただくようご案内することがあります。
※ロマ数トレランにはビデオ視聴以外に欠席保証はございません。ビデオは出席の有無に関わらずご視聴いただけます。

※無料ガイダンス回へのお申し込みはこちらから
ガイダンス回申込フォーム

∞企画運営∞

和から株式会社
渋谷（本社）・新橋・大阪にて社会人向けの数学個別指導教室「大人のための数学教室 和（なごみ）」や「大人のための統計教室和」を運営。数学が苦手な大人から 数学の業務・研究応用を 目的としているマーケター、経営者、大学教授まで月間400名を超える社会人に対して必要な数学や統計学の授業を日々提供している。企業におけるデータセンス研修やデータ分析研修も実施。
和から株式会社HPはこちら>>

∞お問い合わせ∞

和から株式会社  松中宏樹
MAIL：class@wakara.co.jp