ロマンティック数学ナイト

※本セミナーは終了しました。数学教室和(なごみ)の個別授業で受講可能です。詳細はこちらからご確認ください。
⇒個別授業「微分トポロジー」

ロマ数トレランの詳細については次のページ内リンクをご覧ください。ロマ数学トレランとは>>
　

∞セミナーの目的∞

・「微分位相幾何学」V.Guillemin /A.Pollack著、三村護 訳（現代数学社）の第1章を読み、高次元の世界を調べるためのいくつかの数学的手法を身に付ける。
・「はめ込み」や「埋め込み」について理解し、交差理論の有用性を知る。

∞セミナーの概略∞

高次元の世界は目に見えないため、実際に長さを計ったりして調べることはできません。そこで、逆関数定理、モース関数、サードの定理などを用いると、見えない空間を「輪切り」にして調べることができます（下図）。

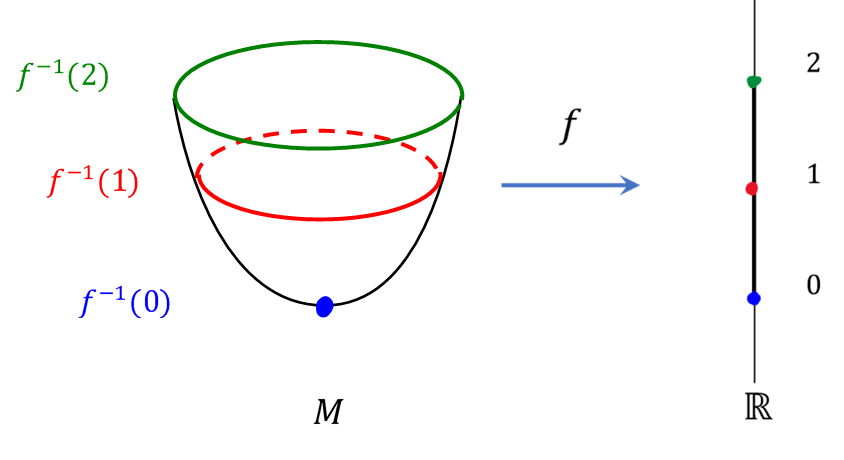
また、接空間や接バンドルを考えることにより、有名な「ホイットニーの埋め込み定理」を少し弱い形で証明します。さらに通常はホモロジー論を用いて証明する「\(2\)次元実射影平面が\(3\)次元空間には埋め込めない」ことの証明を交差理論を用いて行い、この結果を用いて「The Inscribed Rectangle Problem（隠れ長方形問題、詳細はhttps://wakara.co.jp/mathlog/20200809-2）」という具体的な問題を解決します。

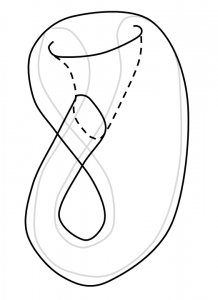
多様体（ここでは「世界」と表現）の\(n\)次元空間への「埋め込み」とは、わかりやすく言うと、「\(n\)次元空間内にもとの形を壊さずに世界全体を実現する」ことです。一方「はめ込み」とは自己交叉があったりして、少し姿が変わってしまうような実現のしかたを指します。例えば、下左図は、円周の平面への「はめ込み」、右図は「埋め込み」を表しています。

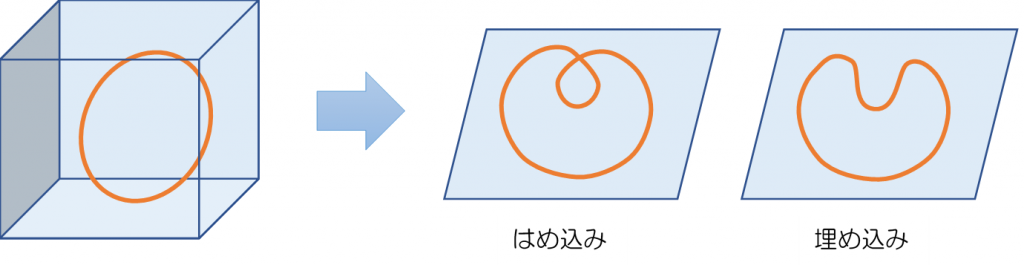
「ホイットニーの埋め込み定理」とは、「どんな世界でも、\(2\)倍の次元の真っ直ぐな空間の中に埋め込める」という定理で、Whitneyはこのことを有名な「ホイットニーの手品」の手法を用いて証明しました。

上図のように、「\(1\)次元の世界」のひとつである円周は2次元平面には「埋め込み」できますが、\(1\)次元の直線内に入れると必ずつぶれてしまいます。また、クラインの壺（これは「\(2\)次元の世界」のひとつ）は\(3\)次元空間内ではどうしても自己交叉ができてしまいますが、\(2\times 2=4\)の\(4\)次元以上の空間であれば、自己交叉のない形で実現できる（はず）、ということになります。つまり我々の想像力をあと\(1\)次元だけ広げることができればクラインの壺の本来の姿を見ることができるのですね。

\(2\)次元実射影平面（cross cap）も非常にイメージしにくい代物ですが、\(4\)次元空間の中であれば本来の自己交叉のない姿が実現できるとわかります。ホイットニーの定理は任意の次元数\(n\)に対してこのようなことが成り立つ、つまり\(n\)次元の多様体は\(2n\)次元のユークリッド空間に必ず埋め込める、ということを保証してくれます。授業ではこの少し弱い形（\(2n+1\)次元への埋め込み）について、Sardの定理と接バンドルの理論を用いた別証明を与えます。

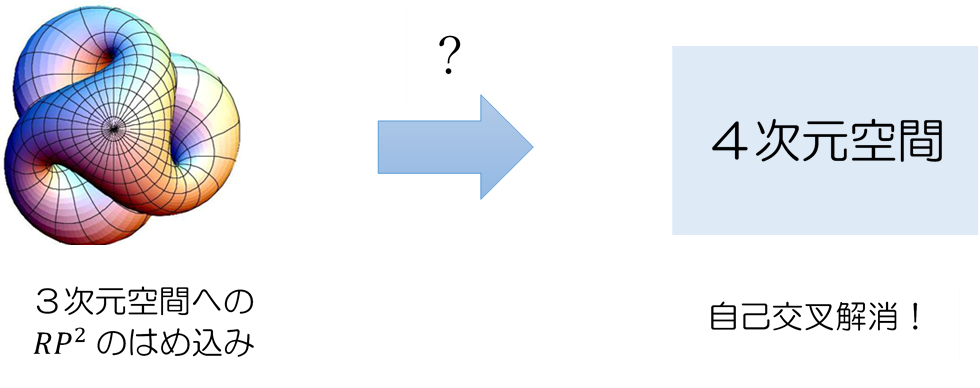
さらに、\(2n\)次元の最小性を示す例として、２次元の実射影平面が\(2×2-1=3\)次元空間には絶対に「埋め込めない」つまり自己交叉を解消できないことを交差理論によって証明したいと思います。数学では「何かが絶対にできない」ことの証明は大変難しいもので、「もしできたとしたら矛盾が起きる」という背理法に持ち込むしかありません。その矛盾を示すために「交点数の偶奇」を調べます。

テキストの第２章以降には、このような「交差理論」により、通常は（コ）ホモロジー論などの大掛かりな体系を学んでからでないとお目にかかれない様々な大定理の証明が載っています。時間の関係上、今回のトレランでは第１章までしか扱えませんが、その有用性の片鱗だけでもお見せしたいと思います。また、「埋め込めない」という結果の応用例として、「The Inscribed Rectangle Problem」を取り上げます。

大学院レベルの内容ですが、演習問題を実際に解きながら読み進め、高次元の世界を感じていきましょう。演習問題の一部は受講生の皆さんにも解いていただく予定です。今回のトレランで身に着く交差理論などの手法を用いて、様々な大定理を証明していく続編セミナーを予定しています。

∞微分トポロジーとは∞

「エキゾチック球面」「モース理論」「\(C^\infty\)多様体」「ベクトルバンドル（ベクトル束）」「ファイバーバンドル（ファイバー束）」「葉層構造(foliation)」「特性類」「同境理論」などに関係する数学の分野です。微分位相幾何学とも言われます。微分幾何学（曲率や接続、ゲージ理論、リーマン多様体などに関係）とは異なる分野です。

微分トポロジーやテキストで取り扱っている定理など、詳しくはマスログでご参照ください。
https://wakara.co.jp/mathlog/20210302(佐々木先生書下ろしの記事)

∞セミナーの進め方∞

隔週開催、1回2時間半×10回のオンライン授業で、V.Guillemin /A.Pollack の「微分位相幾何学」の第一章、「多様体の基礎」付録Bを解説します。テキストには必須の演習問題（＊印）が多数あります。一部は授業中に解説し、解説し切れなかった部分は受講生の皆さんの課題とします（希望者のみ、あるいは全員１問ずつなど）。課題の解答はオンラインホワイトボードにて受講生全員と講師で共有します。授業では、数学記号（ ∀ f:X→Y など）や可換図式を使います（下図）。

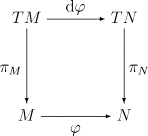
∞教科書∞

「微分位相幾何学」 V.Guillemin /A.Pollack著、三村 護 訳（現代数学社1998）

または
原著Differential Topology V.Guilleman, A.Pollack (Pearson College Div 1974)

∞参考文献∞

解析入門I、II（杉浦）、線形代数入門（斎藤）、集合・位相-基礎から応用まで（佐久間）、Introduction to TOPOLOGY(Bert Mendelson)、多様体の基礎（松本）、微分トポロジー講義 ( J.W.Milnor蟹江訳 Topology from the Differentiable Viewpointの訳書 以下のURLに原著PDFがあります)
https://math.uchicago.edu/~may/REU2017/MilnorDiff.pdf

∞セミナー内容（学習する項目）∞

※全10回で以下のトピックを解説していく予定です。

・多様体、滑らか、微分同相写像、助変数化（パラメトリゼーション）、座標関数、部分多様体、立体射影、積写像、対角集合、グラフ
・連鎖律、可換図式、接空間、接ベクトル、曲線、速度ベクトル
・逆関数定理、はめ込み、固有写像、埋め込み
・しずめ込み、逆像、正則値、逆像定理、臨界値、（関数の）独立、余次元、レコードの積み重ね定理
・横断的、レフシェッツ不動点、レフシェッツ写像
・ホモトープ、ホモトピー、ホモトピー類、安定的、安定類、安定性定理、弧状連結、可縮、単連結
・Sardの定理、測度零、非退化臨界点、Morseの補題、Morse関数
・導関数写像、１の分割、Whitneyの埋め込み定理、ベクトル場、切断、零点
・実射影平面\(RP^2\)が3次元空間\(R^3\)に埋め込めないこと、「The Inscribed Rectangle Problem」

∞講師∞

佐々木　和美（ささき　かずみ）

1972年　広島県生まれ。
1992年頃　東京大学理学部数学科にて、古田幹夫、深谷賢治、坪井俊、松本幸夫、加藤和也、斎藤毅、河東泰之、小林俊行、大島利雄、落合卓四郎（敬称略）など（今思えば）錚々たる先生方から数学を教わる。学部3年で深谷先生の双曲幾何、学部4年で黒川信重先生の代数幾何セミナーに参加するが、最終的にトポロジーを専攻。大学院では松本幸夫先生に師事し、曲面のMapping Class Groupを学ぶ。
家庭教師（大学受験生、高専生ほか）、数学教室　和（なごみ）講師、工業高専非常勤講師など。やさしく楽しい教え方に定評がある。
書籍の校閲・校正 多数（石井俊全氏、堀口智之氏ほか）
ロマンティック数学ナイトガールズ登壇（2017）
夫、三女、猫、金魚。
趣味は、コントラクトブリッジ（JCBLブリッジインストラクター）
　

∞受講対象∞

1.偏微分、重積分、ベクトル、行列と行列式、線形空間、開集合、連結、コンパクト、写像、全単射、直積などについて学んだことがある方
2.高次元の世界や、厳密な証明に興味のある方
3.実際に手を動かして問題を解く努力のできる方

∞開催場所∞

オンライン(zoom)

※好きな場所でご受講できます。「zoom」を用いてオンラインでセミナーを行います。
※ブラウザが利用できるPCやタブレットなどの環境をご用意ください。
※iPad等タブレットの使用は一部機能が制限される場合がございます。パソコン端末でのご参加を推奨いたします。

∞開催日時∞

第0回2021年3月16日(火) 20時00分～21時30分（ガイダンス回・無料）
第1回 3月30日(火) 20時00分～22時30分
第2回 4月13日(火) 20時00分～22時30分
第3回 4月27日(火) 20時00分～22時30分
第4回 5月11日(火) 20時00分～22時30分
第5回 5月25日(火) 20時00分～22時30分
第6回 6月8日(火) 20時00分～22時30分
第7回 6月22日(火) 20時00分～22時30分
第8回 7月6日(火) 20時00分～22時30分
第9回 7月20日(火) 20時00分～22時30分
第10回 8月3日(火) 20時00分～22時30分

※3月16日の第0回は3月30日開講の本セミナーのガイダンス回となります。
※第0回に参加しなくても第1回目以降は申し込むことは可能です。
※セミナー時間150分の内、30分は受講生からの質問、議論に充てられるように設計しています。
※各セミナーの録画をゼミ最終回の1か月後まで視聴できるようにしますので、欠席の回があっても問題ありません。

∞お持ち物∞

筆記用具（ペン、ノートなど）
教科書「微分位相幾何学」V.Guillemin /A.Pollack著、三村護 訳（現代数学社）をご用意ください

∞料金とお申し込みに関して∞

・ガイダンス回(3月16日)  無料
⇒お申込み(https://peatix.com/event/1841624/view)
・本セミナー(全10回)  65,500円(早期割引:62,500円)
⇒お申込み(googleフォーム)

※セミナーの性格上本セミナーの定員は8名とさせていただきます(先着順)。
※本セミナーお申し込みの方に振込先の口座をご連絡いたします。
※最小履行人数は4名となります。最小履行人数に満たない場合、非開催となり、料金は返金させていただきます。開催有無は第一回ゼミの1週間前である3月23日に確定となります。
※早期割引はガイダンス回翌日までに全回お申し込みの方に適用いたします。
※日程、時間の都合でガイダンス回に参加できない方は、担当の松中(メール：class@wakara.co.jp)までご連絡ください。ガイダンス回当日中に録画した動画を視聴できるように手配いたします。ただし、早期割引が適用されるのはガイダンス回の翌日までとなりますので、予めご了承ください。

∞本セミナー受講希望者の方向けの注意事項∞

・通信トラブル等が発生した時に、講師、受講生で円滑に連絡を取り合えるようLINEグループを作成します。LINEグループへの参加は必須とさせていただきますので、予めご了承ください。
・オンラインセミナー受講の際に必要となるパソコン、タブレットまたはスマホ等の通信機器、およびWiFi等のインターネット接続サービスは受講生ご自身でご準備いただきます。
・Apple Pencilなどのスタイラスペンやペンタブなど、画面にペンによる書き込み、描画を行える環境をご準備いただくことを推奨いたします。
・各セミナーの録画動画を最終回の1か月後まで視聴できるようにしますので、出席できない回は動画での受講が可能です。
・欠席者には録画動画だけでなく、セミナーで使用する配布資料(pdfファイルやurl等)も出席者同様配布いたします。

∞ロマ数トレランとは∞

「時間はかかってもいいから数学の美しさを中身からしっかり理解したい！」
聞いているだけでわくわくする華やかなテーマが満載のロマンティック数学ゼミ。
その根底となる理論からしっかり学びたい。ロマ数トレランはそんな声から生まれました。

ロマ数トレランは、ロマン溢れる数学を語ることができる講師による、講義形式ではなく、双方向の対話に重きをおいた受講者参加型の少人数制ゼミです。
実際に手を動かしたり、しっかりと質問、議論をする時間を設けることで
内容を確実に理解することを目標とします。同じ気持ちをもった仲間と一緒に学んだ先には新しい数学の世界が待っています。

～トレランとは～
山を縦走する山岳レースを意味するトレイルランニングの略です。
急坂は大変な時はありますが、いったん頂上に上がれば壮大な風景を楽しむことができます。
数学も同じです！平坦な道も、下り坂も、そして時にはハードな時もありますが、頑張って登りきれば素晴らしい風景が広がっているのです！

※ロマ数トレランでは受講生の理解に合わせて講師が適切な速度になるよう誘導しますが、受講者の理解を優先するため、カリキュラムの進度は確約いたしかねますので、予めご了承ください。
※質問の内容がセミナーの趣旨とそれる場合や、セミナーの適切な進行の妨げになると講師が判断した場合には、解説はセミナー内ではなく別途個別指導をご受講いただくようご案内することがあります。
※ロマ数トレランにはビデオ視聴以外に欠席保証はございません。ビデオは出席の有無に関わらずご視聴いただけます。

※無料ガイダンス回へのお申し込みはこちらから
https://peatix.com/event/1841624/view

∞企画運営∞

和から株式会社
渋谷（本社）・新橋・大阪にて社会人向けの数学個別指導教室「大人のための数学教室 和（なごみ）」や「大人のための統計教室和」を運営。数学が苦手な大人から 数学の業務・研究応用を 目的としているマーケター、経営者、大学教授まで月間400名を超える社会人に対して必要な数学や統計学の授業を日々提供している。企業におけるデータセンス研修やデータ分析研修も実施。
和から株式会社HPはこちら>>

∞お問い合わせ∞

和から株式会社  松中宏樹
MAIL：class@wakara.co.jp